Curiosidades matematicas: soluciones

*Prueba tu habilidad con los números:
    a)¿Sabrías escribir el número 10 de dos formas distintas empleando cuatro nueves?
                       10=(9x9+9)/9
                        10=(99-9)/9

    b)¿Sabrías escribir el número 100 de cuatro modos distintos empleando cinco cifras iguales?.
    Ejemplo: 100=111-11.

                        100=33x3+(3/3)
                        100=[(44-4)/4]^{raíz cuadrada de 4}

    c)¿Puedes escribir el número 30 con tres treses?. ¿Y con tres seises?. ¿Y con tres cincos?.
                                30=33-3
                                30=6x6-6
                                30=5x5+5

SOLUCIÓN ACTIVIDAD 2

En primer lugar descomponemos el número 36 como producto de tres números naturales y calculamos la suma de los tres factores:

                36= 1.1.36 (suma 38)            36= 1.2.18 (suma 21)
                36= 1.3.12 (suma 16)            36= 1.4.9 (suma 14)
                36= 1.6.6 (suma 13)            36= 2.2.9 (suma 13)
                36= 2.3.6 (suma 11)            36= 3.3.4 (suma 10)

Naturalmente, nuestro amigo conoce el número de su casa. Entonces, ¿porqué dice que le falta un dato?. Evidentemente, el número de su casa es el 13 que es la única suma repetida en la serie anterior y en consecuencia necesita conocer algo mas sobre los hijos de su amigo. Quizás desconcierte un poco la respuesta de su amigo pero tiene su explicación. Si observamos los dos productos 1.6.6 y 2.2.9 veremos que en ambos aparecen dos números repetidos (hermanos gemelos o mellizos),en este momento comprendemos que la respuesta "La mayor toca el piano" nos conduce a la solución "2,2,9" ya que la otra alternativa es imposible.

SOLUCIÓN ACTIVIDAD 3

Vamos a utilizar un poco de cálculo algebraico. Supongamos que el número de tres cifras es "abc".Expresamos este número como potencias de 10: a.10²+b.10+c. En orden inverso seria   cba= c.10²+b.10+a.
Los restamos (suponiendo a>c):
(a.10²+b.10+c)- (c.10²+b.10+a)=(a-c).10²+(c-a)=
(a-c)(100-1)=(a-c).99.
Es decir, siempre se obtiene un múltiplo de 99. Analicemos estos múltiplos:
        99.1=99=099
        99.2=198
        99.3=297
        99.4=396
            .
            .
Observamos que todos tienen propiedades comunes:
        *la cifra de las decenas siempre es un nueve
        *la cifra de las unidades y las centenas suman nueve
Es evidente que nos basta con conocer la cifra de las unidades (o centenas) para "adivinar" el número resultante.

SOLUCIÓN ACTIVIDAD 4

Utilizamos de nuevo el cálculo algebraico. Supongamos que el número de tres cifras es "abc". Escrito como potencias de 10: a.10²+b.10+c. Escribimos el mismo número a continuación: "abcabc".
Es decir, abcabc= a.10⁵+b.10⁴+c.10³+a.10²+b.10+c=
a(10⁵+10²)+b(10⁴+10)+c(10³+1)=
=a.10²(10³+1)+b.10(10³+1)+c(10³+1)=
(a.10²+b.10+c).1001
El resultado siempre es el número inicial multiplicado por 1001.
Descomponiendo el número 1001 en factores primos se obtiene que 1001=7.11.13 con lo cual queda aclarado el resultado de este juego.

SOLUCIÓN ACTIVIDAD 5

La herencia del Jeque
En primer lugar hagamos unas cuantas reflexiones sobre el problema:
* Si sumamos una mitad, una tercera parte y una novena parte, no se obtiene el total de los 17 camellos (debería ser 17/17)
Efectivamente:
1/2 + 1/3 + 1/9 = (9+6+2)/18 = 17/18
* El número 17 (primo) no es múltiplo común de 2, 3 y 9.
* Se debe hacer el reparto sin matar ningún camello.
Evidentemente, el problema no tiene solución tal y como se presenta. Sin embargo, el cadí intentó dar una solución lo mas aproximada posible y que dejase contentos a los hijos. Se dio cuenta que añadiendo otro camello se obtenía un número (18) múltiplo de 2, 3 y 9 que permitía hacer el reparto exacto y además le permitía recuperar el camello añadido (la suma de las tres fracciones era 17/18, de 18 camellos se repartían 17).

SOLUCIONES ACTIVIDAD 6

Números consecutivos
a)¿Es posible generar todos los números entre 1 y 30, por suma de números consecutivos?.

b)¿Cuáles son los números que pueden generarse por suma de 2 consecutivos?
*Los números primos solo pueden generarse por suma de dos consecutivos.(3, 5, 7, 11, 13, 17, 19, 23, 29).
*Los múltiplos de 3 o de 5 que no sean pares (9, 15, 21, 25, 27).

c)¿Cuáles pueden generarse por suma de 3 consecutivos?
*Los múltiplos de 3 (6, 9, 12, 15, 18, 21, 24, 27, 30).

d)¿Es posible generar un número entre 1 y 30 por adición de 4 consecutivos?
*10, 14, 18, 22, 26, 30.

e)¿Es posible predecir qué números entre 1 y 100 pueden generarse sumando números consecutivos?
Teniendo en cuenta lo anterior y algunas propiedades mas:
*Los números potencias de 2 no se pueden descomponer.
*Los números 15, 20 ,25 ,30 ,... se pueden descomponer como suma de cinco consecutivos.

SOLUCIÓN ACTIVIDAD 7

Se toma una moneda del primer saco, dos monedas del segundo, tres del tercero, y así sucesivamente hasta coger ocho monedas del octavo saco. De esta forma tendremos 36 monedas, las cuales pesaremos. si todas ellas fueran auténticas pesarían 360 gramos, pero como hemos tomado alguna moneda del saco de las falsas el peso total será menor, y esto nos permitirá averiguar cuál es le saco que contiene las monedas falsas. Si falta un gramo para los 360, el saco de las falsas es aquel del que cogimos una moneda, si faltan dos gramos es el saco del que tomamos dos, si faltan tres es el tercero, etc.

SOLUCIÓN ACTIVIDAD 8

Basta con que haga dos pesadas. En la primera pesa seis monedas, poniendo tres en cada platillo, pudiendo darse dos casos:

1) Si pesan igual las de un lado como las del otro, la falsa está entre las tres no pesadas, y en tal caso se aparta una de ellas y pesando las otras dos se averigua cuál es la moneda falsa.

2) En el supuesto de que en la primera pesada se inclinara la balanza hacia un lado indicaría que la moneda falsa estaba en el lado contrario y en este caso en la segunda pesada se hace la operación de pesar dos monedas del grupo en que sabemos se encuentra la falsa.

SOLUCIÓN ACTIVIDAD 9

Puedes encontrar muchas soluciones. Te propongo un par de cuadrados mágicos.

2	12	5	15	1	15	14	4
13	7	10	4	12	6	7	9
11	1	16	6	8	10	11	5
8	14	3	9	13	3	2	16

Te sugiero un método para construir el cuadrado de la derecha.
Se cuentan las casillas en el orden normal, comenzando por la primera situada en la parte superior izquierda, pero solamente se anotan los números correspondientes a los cuadritos de las cuatro esquinas y a los cuatro centrales. Para escribir los números que corresponden a las casillas que quedan en blanco se procederá de igual modo, pero esta vez comenzando por la casilla 16 y continuando del 1 al 16 siguiendo las casillas en orden inverso y anotando los números correspondientes en los cuadritos en blanco.

1			4	1	15	14	4
	6	7		12	6	7	9
	10	11		8	10	11	5
13			16	13	3	2	16

SOLUCIÓN ACTIVIDAD 10

SOLUCIÓN ACTIVIDAD 11

SOLUCIÓN ACTIVIDAD 12

El tema se hizo muy popular y llegó a oídos de Euler, matemático suizo nacido en Basilea en 1707, quien demostró que era imposible recorrer los siete puentes sin pasar dos veces por uno de ellos.
Para comprobarlo, identificó cada una de las orillas con un punto e hizo lo mismo con cada una de las islas, convirtió los puentes en líneas que unían los puntos; de esta forma obtuvo una red de puntos y líneas.

En una red de este tipo, se denominan vértices pares a aquellos a los que llega un número par de líneas, e impares si es un número impar.
Euler demostró que era imposible recorrer una red sin pasar dos veces por el mismo camino (línea) si ésta tenía más de dos vértices impares. En el caso de que sólo hubiera dos vértices impares, era posible recorrer la red si se partía de un vértice impar y se acababa en el otro.
Por lo que respecta a los puentes, todos los vértices son impares (a todos llegan tres caminos, excepto a una de las islas que llegan cinco), por tanto, el problema no tiene solución.

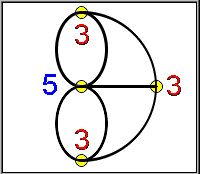
Puedes comprobar que el problema tendría solución, por ejemplo, eliminando el puente que une las dos islas y tomando como punto de partida una de las orillas y como punto de llegada la otra ya que, eliminando el puente intermedio, tendríamos dos vértices impares y dos pares.

SOLUCIÓN ACTIVIDAD 13

Basta con encontrar el único año (del siglo XIX) que es un cuadrado perfecto: 1849 = 43²

3=1+2	17=8+9
4	18=5+6+7=3+4+5+6
5=2+3	19=9+10
6=1+2+3	20=2+3+4+5+6
7=3+4	21=10+11=6+7+8=1+2+3+4+5+6
8	22=4+5+6+7
9=4+5=2+3+4	23=11+12
10=1+2+3+4	24=7+8+9
11=5+6	25=12+13=3+4+5+6+7
12=3+4+5	26=5+6+7+8
13=6+7	27=13+14=2+3+4+5+6+7=8+9+10
14=2+3+4+5	28=1+2+3+4+5+6+7
15=7+8=4+5+6=1+2+3+4+5	29=14+15
16	30=6+7+8+9=4+5+6+7+8=9+10+11

1=2+2-2-2/2	6=2+2+2+2-2
2=2+2+2-2-2	7=(22/2)-2-2
3=2+2-2+2/2	8=2x2x2+2-2
4=2x2x2-2-2	9=2x2x2+2/2
5=2+2+2-2/2	10=2+2+2+2+2

SOLUCIONES

SOLUCIONES ACTIVIDAD 1