ACTIVIDAD 1

Descomponer números
*Uno de los mayores entretenimientos matemáticos es el de descomponer un cierto número de varias formas.
Por ejemplo, ¿sabías que el número 1729 es el primer número que se descompone como suma de dos cubos perfectos, de dos maneras distintas?.
Efectivamente, puedes comprobar que 1729=10³+9³=12³+1³

*Prueba tu habilidad con los números:
    a)¿Sabrías escribir el número 10 de dos formas distintas empleando cuatro nueves?
    b)¿Sabrías escribir el número 100 de cuatro modos distintos empleando cinco cifras iguales?.
        Ejemplo: 100=111-11.
    c)¿Puedes escribir el número 30 con tres treses?. ¿Y con tres seises?. ¿Y con tres cincos?.

Solución 
Índice

ACTIVIDAD 2

Problema de las edades
Dos amigos mantienen esta conversación:
-¿Cuántos años tienen ya tus tres hijos?-pregunta el primero.
-Seguro que lo aciertas -contesta el segundo-. El producto del número de años que tienen es 36 y su suma es igual al número de tu casa.
-Me falta un dato -dice el primero transcurrido un instante.
-Ah, ¡es verdad! -reconoce el segundo-. La mayor toca el piano.

¿Sabrías decir las edades de los tres hijos?.

Solución
Índice

ACTIVIDAD 3

Jugando con números
Te planteo este sencillo juego.
-Escribe un número de tres cifras distintas.(Por ejemplo 136.)
-Escríbelo en orden inverso (631).
-Resta del mayor el menor (631-136=495)
-Si tu me dices la cifra de las unidades, yo adivino el valor de la resta.

¿Crees que es posible?.

Solución
Índice

ACTIVIDAD 4

Seguimos jugando con números
-Piensa un número de tres cifras y escríbelo.
-Escribe el mismo número a continuación del anterior. Habrás obtenido un número de seis cifras.
-Comprueba si ese número es divisible entre 7 haciendo la operación.
-Averigua si el nuevo cociente es divisible entre 11. Divídelo.
-Divide el nuevo cociente entre 13.
-¿Has obtenido como cociente el número pensado?

Solución
Índice

ACTIVIDAD 5

La herencia del Jeque
Un Jeque árabe tenía tres hijos y les dejó al morir 17 camellos, con el mandato expreso de que habían de repartirlos sin matar ningún camello, y de la manera siguiente: El mayor recibirá la mitad; el segundo, la tercera parte, y el menor, la novena parte.
Los hijos del Jeque, al querer hacer el reparto,se dieron cuenta de que para poder cumplir la voluntad de su padre no había mas remedio que descuartizar algunos camellos. Acudieron al cadí, y éste les pidió un día para pensarlo. Pasado ese día, acudió el cadí con un camello suyo y lo unió al grupo de los 17 camellos, y propuso que se procediera a cumplir la voluntad del Jeque sobre esta herencia aumentada. Así, el mayor tomó 9 camellos; el segundo, 6, y el menor, 2. Al terminar el reparto el cadí volvió a llevarse su camello y dejó a los tres hermanos contentos.

Explica la solución dada por el cadí.

Solución
Índice

ACTIVIDAD 6

Números consecutivos
a)¿Es posible generar todos los números entre 1 y 30, por suma de números consecutivos?. Por ejemplo:
                                         6=1+2+3
                                         9=4+5
                                        23=11+12

b)¿Cuáles son los números que pueden generarse por suma de 2 consecutivos?
c)¿Cuáles pueden generarse por suma de 3 consecutivos?
d)¿Es posible generar un número entre 1 y 30 por adición de 4 consecutivos?
e)¿Es posible predecir qué números entre 1 y 100 pueden generarse sumando números consecutivos?

Solución
Índice

ACTIVIDAD 7

Los sacos de monedas
En un banco hay 7 sacos de monedas de curso legal, de un mismo valor, cada una de las cuales pesa 10 gramos. Un empleado, por error, ha dejado junto a estos sacos otro saco de monedas falsas pero idénticas en todo menos en el peso, ya que pesan un gramo menos que las auténticas. ¿Cómo se podrá averiguar cuál es el saco de las monedas falsas haciendo una sola pesada?.

Solución
Índice

ACTIVIDAD 8

Más monedas
Aquí tenemos otro problema de monedas que aunque pueda parecer igual que el anterior no lo es, si bien tiene cierta similitud.
Por descuido, un coleccionista de monedas ha mezclado una moneda falsa con otras ocho monedas de curso legal. Las nueve monedas son idénticas, salvo en el detalle de que la falsa pesa unos centigramos menos que las otras. El coleccionista dispone de una balanza muy sensible y se prepara para pesar las monedas y así poder apartar la falsa, sin emplear pesas. ¿Cuál será el número mínimo de pesadas que deberá hacer para conseguir su propósito?.

Solución
Índice

ACTIVIDAD 9

Los cuadrados mágicos
Los cuadrados mágicos están formados por números colocados de tal forma que las sumas de estos números en filas, columnas y diagonales son iguales, esta suma común se llama número mágico.
El cuadrado mágico representado por Alberto Durero en su célebre grabado "Melancolía" fue descubierto en las ruinas de la ciudad de Khajuraho (siglos X y XI), en la India.

Tal vez Durero eligió este cuadrado porque los dos números centrales de la última fila coinciden con la fecha de ejecución del grabado: 1514.

¿Sabrías encontrar mas cuadrados mágicos similares a este?
 
Solución
Índice

ACTIVIDAD 10

El matemático ignorante
En las aulas de cierta facultad de Matemáticas, nos podemos encontrar a un extraño personaje. Cierto día, me confesó que tan sólo sabía multiplicar y dividir por 2.
- A pesar de todo, me dijo, puedo multiplicar rápidamente números de dos cifras.

Le propuse que multiplicara 75 por 38.
Tomó una hoja de papel y escribió a la izquierda 75 y a la derecha 38. Luego inició sus cálculos:

- La mitad de 75 es 37, ¿no es así?.
- No -le dije- es 37'5.
- De acuerdo, pero no sé trabajar con decimales, así que no los pongo.

Escribió 37 y, repitiendo el proceso, dividió por dos y obtuvo, a pesar de mis protestas, 18, 9, 4, 2 y finalmente 1.
Después multiplicó 38 por dos. El resultado, 76, lo escribió en la fila inferior. Volvió a multiplicar por dos y obtuvo 152, 304, 608, 1216 y 2432.
Al final tenía escrito,

 
Me dijo que los números pares de la columna de la izquierda no servían de nada, así que los tachó (junto con el número que tenían a su derecha) con lo que quedó
 

 
Sumando los números de la columna de la derecha obtuvo: 38+76+304+2432=2850, que es el resultado correcto. Probé con otros números y también funcionaba el método.
¿Sabrías dar una explicación matemática?.

Solución
Índice

ACTIVIDAD 11

Jugando con doses

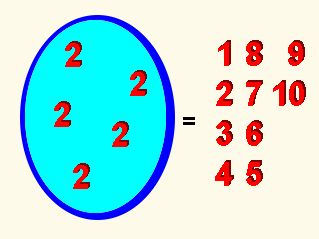
¿Puedes escribir todos los números del cero al diez utilizando cinco doses, y los signos +, -, x, /, además del paréntesis?.  Puedes empezar así    0= 2 - 2/2 - 2/2

Solución
Índice

ACTIVIDAD 12

El problema de los puentes de Königsberg

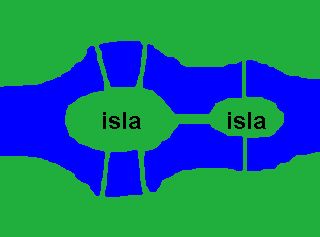
En el siglo XVIII había en la ciudad de Königsberg (situada en la antigua Prusia, hoy Kaliningrado, perteneciente a Rusia) siete puentes que conectaban cada una de las orillas del río Pregel con dos islas interiores. Los ciudadanos estaban muy orgullosos de sus puentes y bromeaban sobre la posibilidad de recorrerlos todos pasando una sola vez por cada uno de ellos.  ¿És esto posible?.

Solución
Índice

ACTIVIDAD 13

Una adivinanza

Augustus de Morgan (¿-1871) fue un matemático inglés nacido en la India. Acostumbraba a recrearse en el planteamiento de adivinanzas y problemas ingeniosos. Este personaje nacido en el siglo XIX, planteaba esta adivinanza sobre su edad: "El año x² tenía x años. ¿En qué año nací?".

Solución
Índice